Tugas 5 Arfan 2103015081 Aljabar Boolean

ALJABAR BOOLEAN

Aturan Aljabar Boolean

Hukum Penjumlahan Komutatif
Penjumlahan Komutatif
A + B = B + A
(The order of OR doesn't matter)

Hukum Perkalian Komutatif
Perkalian Komutatif
AB = BA
(The order of AND doesn't matter)


Hukum Penjumlahan Asosiatif
Penjumlahan Asosiatif
A + (B + C) = (A + B) + C
(The Grouping of OR variables doesn't matter)


Hukum Perkalian Asosiatif
Perkalian Asosiatif
A(BC) = (AB) C
(The Grouping of AND variables doesn't matter)


Hukum Distributif
A(B+C) = AB + AC

(A + B)(C + D) = AC + AD + BC + BD


Aturan Boolean
1). A + 0 = A

  • Dalam matematika jika Anda menambahkan 0 Anda tidak mengubah apa pun
  • Didalam Aljabar Boolean logika OR dengan 0 tidak mengubah apa pun.


2). A + 1 = 1

  • Logika OR harus memberikan nilai 1 karena jika inputan adalah 1 maka gerbang OR akan memberikan hasil 1.




    • 3) A . 0 = 0
    • Dalam matematika jika angka 0 dikalikan dengan bilangan apa pun maka akan tetap menghasilkan 0
    • Jika logika AND dengan 0 maka akan mendapatkan hasil 0

    4) A . 1 = A


    5). A + A = A

    • Logika Or akan menghasilkan hasil yang sama
     

                _

    6). A + A = 0


    7). A . A = A

               _

    8). A . A = 0 

  • Dalam logika digital 1 = 0 dan 0 =1, jadi AA= 0 karena salah satu dari input harus bernilai 0.



    • 9) A = ⩞ 



    10) A + AB = A

    Contoh : 
    A + AB = A (1 + B)     Distributive Law
                 = A . 1             Rule 2 : (1+B) = 1
                 = A                  Rule 4 : A . 1 = A


    11) A + AB = A + B
    • Jika A adalah 1 dan output bernilai 1, jika A adalah 0 maka outputnya adalah B
    Contoh :
    A + AB = (A + AB) + AB                 RULE 10
                 = (AA + AB) + AB              RULE 7
                 = AA + AB + AA + AB        RULE 8
                 = (A + A) ( A + B)                FACTORING
                 = 1 . (A + B)                         RULE 6
                 = A + B                                 RULE 4


    12). (A + B) (A + C) = A + BC

    Contoh :
    (A + B)(A+C) = AA + AC + AB + BC            DISTRIBUTIVE LAW
                            = A + AC + AB + BC            RULE 7
                            = A(1+C) + AB + BC            FACTORING
                            = A . 1 + AB + BC                RULE 2
                            = A(1 + B) + BC                   FACTORING
                            = A . 1 + BC                          RULE 2
                            = A + BC                               RULE 4
    https://onlinelearning.uhamka.ac.id

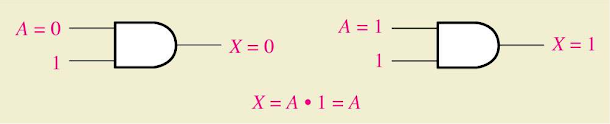
    Komentar

    Posting Komentar

    Postingan populer dari blog ini

    Tugas 4 Arfan 210301508 Gerbang Logika

    Gerbang logika Gerbang Logika dan Aljabar Boolean Aljabar Boolean adalah alat yang penting dalam menggambarkan, menganalisa, merancang, dan mengimplementasikan rangkaian digital Konstanta Boolean dan Variabel l    Aljabar Boolean dibawah ini hanya  mempunyai dua nilai : 0 dan 1. l    Logika 0 dapat dikatakan : false, off, low, no,  saklar terbuka. l    Logika 1 dapat dikatakan: true, on, high, yes,  saklar tertutup. l    Tiga operasi logika dasar: OR, AND, dan  NOT. Tabel Kebenaran l    Sebuah tabel kebenaran menggambarkan  hubungan antara input dan ouput sebuah  rangkaian logika. l    Jumlah The number of entries corresponds to  the number of inputs.  For example a 2 input  table would have 2 2  = 4 entries. A 3 input  table would have 2 3  = 8 entries. Gerbang Logioka Operasi OR dengan gerbang OR The Boolean expression for the OR operation is              X = A + B            This is read as “x equals A or B.”             X = 1 when A = 1 or B = 1   OR Operation With OR Gates l    Th
    Baca selengkapnya

    Tugas 8 Arfan 2103015081 Function of CL

    Function of CL   Fungsi Kombinasi Logika  Penjumlahan binary sederhana  0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Basic adder      Adder penting dalam komputer dan juga dalam jenis sistem digital lainnya di mana data numerik diproses. H alf adder menerima dua digit biner pada inputnya dan menghasilkan dua digit biner pada outputnya, bit jumlah dan bit carry. The Full adder      Full-adder menerima dua bit input dan input carry dan menghasilkan jumlah output dan output carry. Penambah penuh harus menambahkan dua bit input dan input membawa.      Dari setengah penambah, jumlah bit input A dan B adalah eksklusif-OR dari kedua variabel tersebut. Untuk masukannya carry (Cin) untuk ditambahkan ke bit input, itu harus eksklusif-ORed, dan terakhir menghasilkan persamaan untuk jumlah output dari penambah penuh     Ini berarti bahwa untuk mengimplementasikan fungsi penjumlahan penambah penuh, dua gerbang OR eksklusif 2-masukan dapat digunakan. Yang pertama harus menghasilkan istilah A+B dan yang
    Baca selengkapnya